|
|
|

DETERMINACIÓN DE LA PREDECIBILIDAD
DE TRAZAS DE
TRÁFICO MEDIANTE ANÁLISIS DE RECURRENCIA
GRAFICO DE RECURRENCIA

El Gráfico de Recurrencia (GR) es una herramienta de análisis que revela la existencia de patrones recurrentes e intermitentes en series de tiempo. Propuesto por primera vez por Echan [13], ha tenido gran aplicación en la caracterización de sistemas dinámicos.El objetivo del gráfico de recurrencia es encontrar la repetición de un patrón dentro del espacio de estados de un sistema. Aunque un proceso no sea periódico en sentido estricto es posible que muestre comportamientos repetitivos o ‘recurrentes’. Una de laS formas de caracterizar esta recurrencia consiste en comparar la diferencia entre todos los estados de la trayectoria que describe la evolución del sistema.A continuación ampliaremos y precisaremos el contexto de aplicación de conceptos como: espacio de estados, espacio de estados reconstruido, trayectoria y recurrencia. Finalmente aplicaremos estos conceptos a series de datos autosimilares.
1.1 ESPACIO DE ESTADOS
Un sistema dinámico puede describirse por sus variables de estado.
El conjunto de m variables de estado forma un vector xQ) en un espacio , m-dimensional, espacio conocido como espacio de fases. La evolución en el tiempo de este vector forma una trayectoria u órbita en el espacio de fases y la evolución de la trayectoria indica la dinámica del sistema.
Usualmente no es posible obtener todas las variables de estado que caracterizan un sistema. Algunas veces sólo se dispone de una de ellas. Sin embargo, existe un método para reconstruir la dinámica m-dimensional del sistema a partir del conocimiento de una sola de las variables del mismo. Esto es posible gracias al acoplamiento interno del sistema, que proyecta la dinámica de las variables una sobre la otra. Las consecuencias de ésta propiedad de los sistemas dinámicos son bastante profundas. Por ejemplo, en teoría se podría conocer la dinámica de los océanos de la tierra observando un centímetro de playa.
1.2 MÉTODO DE TAKENS
Un método usado con frecuencia para reconstruir la trayectoria del espacio de fases fue propuesto por Takens [11] y Packard [181, es llamado método de retardos en el tiempo. Dado un sistema dinámico de dimensión m, del cual sólo se conoce la serie u u1, u., u,, que representa la evolución temporal de una de las variables de estado del sistema, es posible construir un Pseudo espacio de fases del sistema, que sea topológicamente equivalente. Es necesario que tal sistema dinámico (de origen) sea determinístico de la forma F(x,, t). La reconstrucción es aplicable sólo en una región A suave de dimensión dA con un número finito de puntos de equilibrio sin órbitas periódicas de período entre t y 2’r, pero con un número finito de órbitas periódicas de período pi t para n entre 3 y m y t entero
El vector de estados de tal reconstrucción estaría dado por:
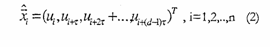
Donde t es un retardo en el tiempo aplicado a u, ti es la dimensión del Pseudo espacio de fases o dimensión reconstruida.
El teorema (le Takens [lii garantiza que si d 2m±1 la estructura topológica de la trayectoria original será preservada en la trayectoria reconstruida; es decir, para obtener un sistema dinámico equivalente al original, se debe cumplir una condición obvia: el pseudo espacio de fases debe tener, por lo menos, la misma complejidad del espacio original. Volviendo a la observación anterior sobre la dinámica oceánica, el espacio de fases reconstruido tendría tantas variables de estado que sería impracticable tal reconstrucción.
La selección de la dimensión de reconstrucción y del retardo en el tiempo es crucial en la generación de ,. Expondremos a continuación los métodos para determinar correctamente tales valores.
1.3 VECINOS PRÓXIMOS FALSOS Y
DIMENSIÓN DE RECONSTRUCCIÓN
Un método para determinar el número de dimensiones en las que se desenvuelve el proceso es conocido como el método de los T/idnos Próximos Falsos [1 61. Supóngase que Aa de dimensión d es el pseudo espacio de fases correspondiente al espacio de fases Bmde dimensión m, tal que d =2m±l. Tórnese un punto b B” que tiene como correspondencia a
e X d en el espacio reconstruido. Corno vimos anteriormente, ambos espacios tiene1 las propiedades topológicas, así que los puntos que estén cercanos a b deben tener sus equivalentes en la cercanía de N. Si la condición d 2m + 1 no se cumple, los puntos vecinos deb serán proyectados muy lejos de N, y la estructura topológica no se preservará.
Si no se conoce de antemano la dimensión menor en que puede ser observada la dinámica del sistema es necesario estimarla construyendo los posibles espacios
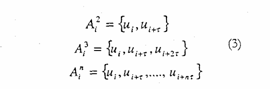

Si se cumple que:
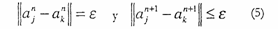
Entonces a y son vecinos próximos verdaderos en A. De lo contrario son vecinos próximos falsos. El test se aplica a todos los puntos pertenecientes al espacio. Si en la dimensión a hay un gran porcentaje de puntos que sean vecinos falsos, entonces a no es una dimensión de reconstrucción adecuada y habría que hacer el test en una dimensión mayor.
1.4 RETARDO EN EL TIEMPO E INFORMACIÒN MUTUA
El siguiente parámetro a elegir es el retardo ‘. La idea a la hora de elegir el retardo de la serie a es bastante sencilla. Supóngase que graficamos un sistema con drn2, tendríamos una gráfica u(’t) Vs oq’t+T). Si
= O evidentemente esta gráfica no aportaría información alguna acerca del comportamiento del sistema., pues seria una línea recta con pendiente 450 En la medida en que sea pequeño las series en los ejes de la gráfica serán muy parecidas y la gráfica obtenida seguirá brindando poca información. El retardo ideal será aquel que maximice la independencia entre u(’t,) y u(t+ ‘y). Una forma de estimar el retardo que produzca esta independencia, sugerida por Fraser [12], se llama Test de Información Mutua.
La Información mutua en función del retardo esta expresada como:

El valor óptimo de ‘r será aquel que minimice a 1 (‘y) . Cuando esto suceda, las dos series serán lo más independiente posible una de la otra. Por lo general se escoge el retardo que produzca el primer mínimo.
1.5 RECONSTRUCCIÓN DE DOS ATRACTORES CONOCIDOS
Veamos un par de ejemplos tomados de un texto tradicional de Teoría del Caos [17]. Se trata de la reconstrucción del Atractor de Lorenz, y de las ecuaciones de Henon. El primer atractor se construye a partir de la integración numérica del sistema de ecuaciones:
En este sistema, las variables de estado son x,j c. La figura 1 ha sido obtenida a partir de la integración numérica del sistema de ecuaciones anterior.
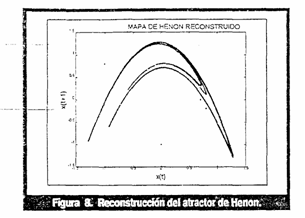
Las variables de estado mencionadas constituyen un atractor en 3 dimensiones que se muestra en la figura 2.En ambos casos podemos apreciar la existencia de una regularidad u orden en los diagramas. Vemos que, aunque el sistema evoluciona y no se detiene en un punto fijo del espacio de fases, tiende a ocupar una región muy definida dentro de este espacio. Ambos son ejemplos de Atractores Caóticos.Apliquemos el procedimiento de reconstrucción antes mencionado al sistema de Lorenz, y al de Henon, escogiendo la serie x(t) como origen de la reconstrucción en ambos casos. El cálculo de la dimensión de reconstrucción d se obtiene a partir del porcentaje de vecinos falsos, mostrado en la tabla 1.Se concluye que la dimensión de reconstrucción óptima es d=2 para el atractor de Henon y d3 para el atractor de LorenzEl retardo óptimo es aquel donde se encuentra el primer mínimo en la información mutua. En la figura se aprecia que el primer mínimo se obtiene para un retardo temporal igual a 17. En la figura 6 se observa que no hay un mínimo relativo, pues la gráfica es monótonamente decreciente, en este caso la teoría recomienda escoger un retardo igual a 2. Las figuras 7 y 8 muestran los atractores reconstruidos en cada caso.
1.6 GRÁFICO DE RECURRENCIA
Como se mencionó inicialmente, el objetivo del GR es encontrar la recurrencia de los estados del sistema, para lo cual se propone analizar las trayectorias del sistema a partir de la reconstrucción en el espacio de estados.Para la construcción del gráfico pueden seguirse dos procedimientos. El primero, llamado Gráfico de Recurrencia sin Umbral, se resume a continuación:
[1]
 Cada punto dentro de la matriz de recurrencia define si la distancia o norma entre los puntos de Y cae dentro del umbral a.
Cada punto dentro de la matriz de recurrencia define si la distancia o norma entre los puntos de Y cae dentro del umbral a.
A partir de la matriz de recurrencia se usan dos colores (blanco y negro por ejemplo) para codificar la recurrencia de los estados. Si el valor X(i,;) es mayor que determinado umbral, entonces el punto en X(i,j) en un espacio bidimensional, es negro, de lo contrario el punto se colorea como blanco. Evidentemente, la elección del valor del umbral u es crítica, puesto que con un umbral muy pequeño el gráfico quedaría saturado y, con un umbral muy grande, el gráfico quedaría prácticamente sin puntos.
El segundo tipo de gráficos son los gráficos sin umbral. La matriz de recurrencia se define como:
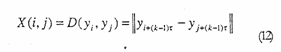 En este procedimiento, el valor de X(i,j) se codifica en una escala graduada en colores. Si se usara una
En este procedimiento, el valor de X(i,j) se codifica en una escala graduada en colores. Si se usara una
escala de grises, un valor alto de Xi,j) significaría un punto de color cercano al negro en la posición (i,j, de un gráfico bidimensional. Un valor cercano a cero de X(i,j), significaría un punto de color cercano al blanco en esta misma posición.
En las figuras 9 y 10 pueden apreciarse los GR con umbral y sin umbral, correspondientes a una serie de datos senoidal.

La figuras 11 y 12 muestran los mismos gráficos para la misma señal contaminada con ruido.

1.7 CUANTIFICACIÓN DE LOS RESULTADOS DEL GR [ROA]
Los resultados de los GR se cuantifican por un procedimiento llamado RQA (Recurreni Quantification Analysis), desarrollado por Zhulut y íí’ebber [15]. A continuación describiremos algunos de los parámetros del RQA aplicados a los GR con umbral.
El primero, denominado Porcentaje de Recurrencia (%REC), es simplemente el número de puntos que hay en el GR, es decir puntos cuyo valor cae dentro de los limites del umbral. Este parámetro se usa para calcular la Dimensión de Correlación CDC) del espacio de fases reconstruido. La DC está definida como la pendiente de la regresión [inca! de la relación entre %REC y el valor del umbral de decisión; es lógico suponer que entre mayor sea el umbral habrá un % de REC menor, y viceversa. La Dimensión de Correlación caracteriza esta relación.
El siguiente parámetro es el Porcentaje de Determinismo (%DEI), el cual está definido como el porcentaje de los puntos del gráfico de recurrencia que se encuentran organizados en líneas paralelas a la diagonal principal, excluyendo la diagonal principal. Estas líneas revelan las semejanzas existentes en el valor de datos cercanos en el tiempo. El %DET, entonces, informa la presencia de interacciones estables en la serie, así como la aparición de órbitas o comportamientos periódicos [131. El %DET indica entonces, qué tan organizado es el proceso bajo observación.
El siguiente parámetro que tiene en cuenta el RQA se denomina Entropía iENT). Se calcula agrupando las líneas diagonales definidas anteriormente, de acuerdo a sus longitudes y usando la siguiente fórmula:
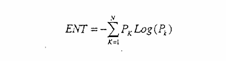 donde N es el número de grupos formados y es el porcentaje de líneas de longitud é. El parámetro ENT está ligado con el %DET, pues la Teoría de la Información demuestra que la predecibilidad disminuye con el aumento de la entropía.
donde N es el número de grupos formados y es el porcentaje de líneas de longitud é. El parámetro ENT está ligado con el %DET, pues la Teoría de la Información demuestra que la predecibilidad disminuye con el aumento de la entropía.
El último de los parámetros que consideraremos es el inverso de la línea máxima (11 L0), donde la línea máxima (LM ) es la línea más larga paralela a la diagonal principal. Se dice en [15] que éste parámetro está directamente relacionado con el inverso del máximo exponente positivo de Lvapunov Valores pequeños de indican comportamiento caótico, valores grandes indican comportamiento periódico.
Estas medidas pueden aplicarse a la serie de datos completa, lo que daría una idea de comportamiento global, o pueden aplicarse ¿e manera local a ventanas de la serie, para observar la evolución de la misma.